1_S6_-_Photo

Et en plus ils travaillent...

Lien

1_S6_-_Logiciel

Logiciel Xcas :
Xcas est un logiciel libre qui permet de pratiquer à la fois le calcul formel, la géométrie dynamique et la programmation (cliquer ici pour plus de détails). Il dispose d'un tableur formel et peut etre amélioré en fonction des demandes des usagers, en particulier pour des raisons pédagogiques.

Lien : http://www-fourier.ujf-grenoble.fr/~parisse/irem.html

Exemple lié au DS01 :

Maths et musique même combat ?

http://en.wikipedia.org/wiki/F%28x%29_%28band%29

1_S6_-_Photos

Ne sont-ils pas beaux ? Photos

Et narcissique en plus !

Je sais, je ne devrais pas ! Mais c'est si bon, juste avant la rentrée !!

Bonne année de terminale (ou autre) à mes anciens 1EN !

Belle application

Ci-dessous l'adresse d'une belle application mathématique en calcul formel :
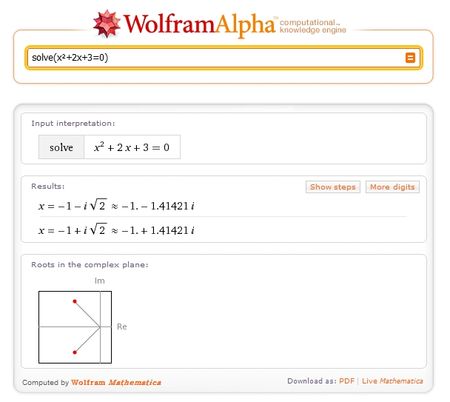
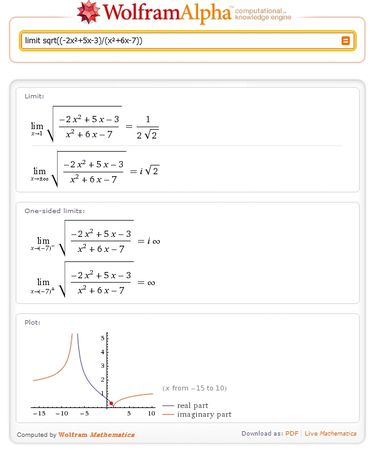
http://www.wolframalpha.com/examples/Math.html


Exemples d'utilisation en maths :

Enigme 27 : suite...

8 ; 7 ; 5 ; 6 ; 3 ; 5 ; 3 ; 0 ; 1 ; 8 ...
On a choisi deux chiffres : le 8 et le 7. On a ensuite écrit les chiffres de leur produit (56) et ensuite le produit du 7 par le 5 à savoir 35 et le produit du 5 par le 6 soit 30...
On continue ainsi en se décalant d'un rang à chaque fois, et en écrivant à la suite les chiffres du produit des deux chiffres considérés (ce produit est toujours un nombre possédant un ou deux chiffres). Au bout d'un temps plutôt long, on n'obtiendra que des zéros.
Quel sera le dernier chiffre non nul ?

Enigme 26 : suite...

Soit une suite de nombres, dont le premier nombre est égal à 1 ainsi que le second et dont chaque nombre est, à partir du quatrième, égal à la somme des trois précédents.
On sait que le treizième nombre de cette suite est égal à 3 667.
Quel est le sixième nombre de la suite ?

Enigme 25 : suite basique

Trouver le dernier terme de la suite suivante :
15 ; 16 ; 17 ; 21 ; 23 ; 30 ; 33 ; 120 ;  ... 

Enigme 24 : Des cimaux

Après avoir péniblement inculqué les notions d'addition et de multiplication à un élève, le frère Carl Friedrich, un éminent moine mathématicien allemand, essaye de lui apprendre à manier les nombres décimaux.
Il lui donne donc 3 nombres comportant chacun un ou deux chiffres après la virgule et lui demande d'en faire le produit, (les chiffres après la virgule ne sont pas égaux à zéro tous les deux).

Mais l'élève trouvant cela trop difficile, se contente de les additionner avant d'annoncer le résultat (sans montrer comment il a fait) : 6,42.
On suppose évidemment que l'addition est juste.
A sa grande surprise, le frère Carl Friedrich le félicite pour avoir trouvé si rapidement le résultat.
Question : quels sont les 3 nombres utilisés ?

                                

Enigme 23 : Triangles rectangles

Certains triangles rectangles ont des valeurs entières pour leurs côtés.
Par exemple (3 ; 4 ; 5) : 3² + 4² = 5²
Ou encore (36 ; 77 ; 85) : 36² + 77² = 85²

Intéressons nous aux périmètres de ces triangles :
        3 + 4 + 5 = 12 pour le premier et
      36 + 77 + 85 = 198 pour le second.

Question : Trouver le(s) triangle(s) rectangle(s) à côtés entiers dont le périmètre est égal à 1000.